Integer constraints

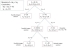
Sometimes, a decision variable cannot be a continuous value, but instead have an integer or binary value. Some examples of this are site open/close decisions, single-sourcing policies, conditional minimum constraints, and anything represented by an integer (such as transportation assets). The initial solution of the problem as outlined above, known as a linear programming relaxation, does not enforce these constraints. Therefore, they must be enforced by branching on this relaxation.

For example, if the solution has x1 = 3.75 and x2 = 2.25 for the integer constrained variables x1 and x2, then a solution is found by branching on this relaxation. Assume the problem is to maximize 9x1 + 5x2 with the following constraints:

9x1 + 5x2 <= 45

x1 + x2 <= 6

The program evaluates integer values for x1, setting x2 to adhere to the constraints. If a valid solution is found, the program then evaluates integer values for x2. It continues to branch on feasible, non-integer solutions. In this case, the optimal integer solution is where x1 = 5 and x2 = 0.

Each variable must be branched on. This happens for every integer variable added to the problem. Each additional integer variable greatly increases the number of potential branch and bound solutions and therefore exponentially increases the time the process takes to run.

In summary, the linear program size and therefore the solving time is affected by decision variables, constraints, and the number of integer variables.