Causal lags

Causal lags represent the delayed effect of a causal variable. Change in a causal's value is not always reflected immediately in demand data. For example, as more electric vehicle charging stations are installed, the demand for electric vehicles increases, which results in higher demand for car batteries. However, in this sequence of events, the effect of one event on another is not instantaneous, and a certain amount of "lag" time exists between pairs of events in the sequence. This delay is referred to a causal lag, and it is important to take this lag into consideration to accurately capture the effect of a causal on demand.

In Demand Guru, the Include Causal Lags parameter calculates 10 lags of each user-defined and Trend Cloud causal, selecting the best lag of each causal. If the selected lag is correlated with the demand time series more closely than the actual causal, then the actual causal time series is replaced by its selected best lag.

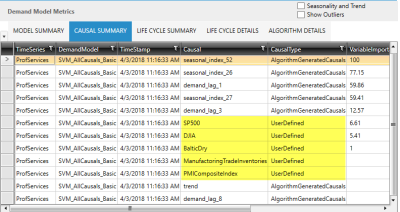
In the following example of a Causal Summary table, the Include Causal Lags parameter is set to False.

Note that 5 user-defined causals (SP500, DJIA, BalticDry, ManufacturingTradeInventories, PMICompositeIndex) are included in the Causal column.

By comparison, the following example shows the same Causal Summary table when Include Causal Lags is set to True.

Note that the causal BalticDry is replaced by BalticDry_lag_6, and ManufacturingTradeInventories is replaced by ManufacturingTradeInventories_lag_2. In these cases, ‘lag 6’ and ‘lag 2’ were the best lags found by the algorithm for their respective causals. Also, observe that the other three user-defined causals (SP500, DJIA and PMICompositeIndex) have not been changed. This means that the present values of these causals affect demand more than any of their lagged values.

In these examples, changing the Include Causal Lags parameter from False to True decreased the Out-of-Sample RMSE from 92.74 to 71.39 and decreased the Out-of-Sample MAPE from 10.97 to 8.29.

The Include Causal Lags parameter is only applicable to the algorithms that can accommodate causal data. It is useful when a machine learning algorithm is used, such as:

• Automatic
• ArimaX
• Model Average Neural Network
• Quantile Random Forest
• Stochastic Gradient Boosting
• SVM Linear
• Tournament

However, this parameter is not effective for classic time series forecasting algorithms such as Auto-Arima or Exponential Smoothing.